Seonglae ChoA convex combination is a linear combination of points where all coefficients are non-negative and sum to 1.
- Weighted average interpretation: A convex combination represents a weighted average of the given points, where the weights (coefficients) indicate the relative contribution of each point.
- Convexity preservation: The result of a convex combination always lies within the convex hull of the original points.
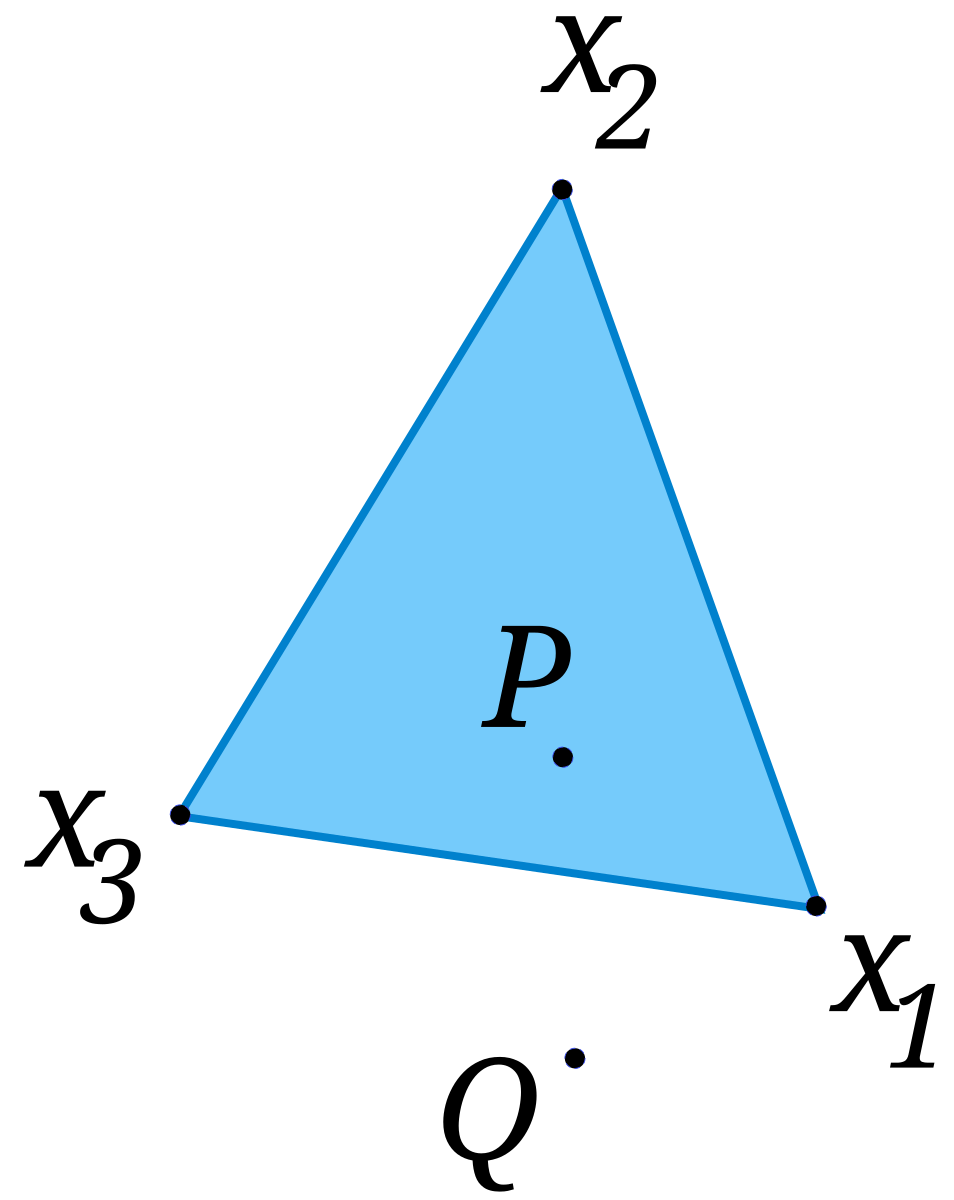
- Geometric meaning: In geometric terms, convex combinations of two points produce all points on the line segment connecting them; for three points, they produce all points within the triangle formed by those points.
Two-point convex combination: For points A and B, the convex combination 0.3A + 0.7B represents a point 70% of the way from A to B.
Centroid: The center of a triangle with vertices at points P₁, P₂, and P₃ is the convex combination (1/3)P₁ + (1/3)P₂ + (1/3)P₃.
Convex combination
In convex geometry and vector algebra, a convex combination is a linear combination of points where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the count of the weights as in a standard weighted average.
https://en.wikipedia.org/wiki/Convex_combination
