Seonglae ChoExponential family distribution over the Probability simplex, essentially a distribution over multinomial distributions.
A set of probability distributions used to model probabilities for each class in multiclass problems and describe proportions
Specific case of Beta Distribution
- controls the mean shape and sparsity of
- Value of create increasingly sparse outputs
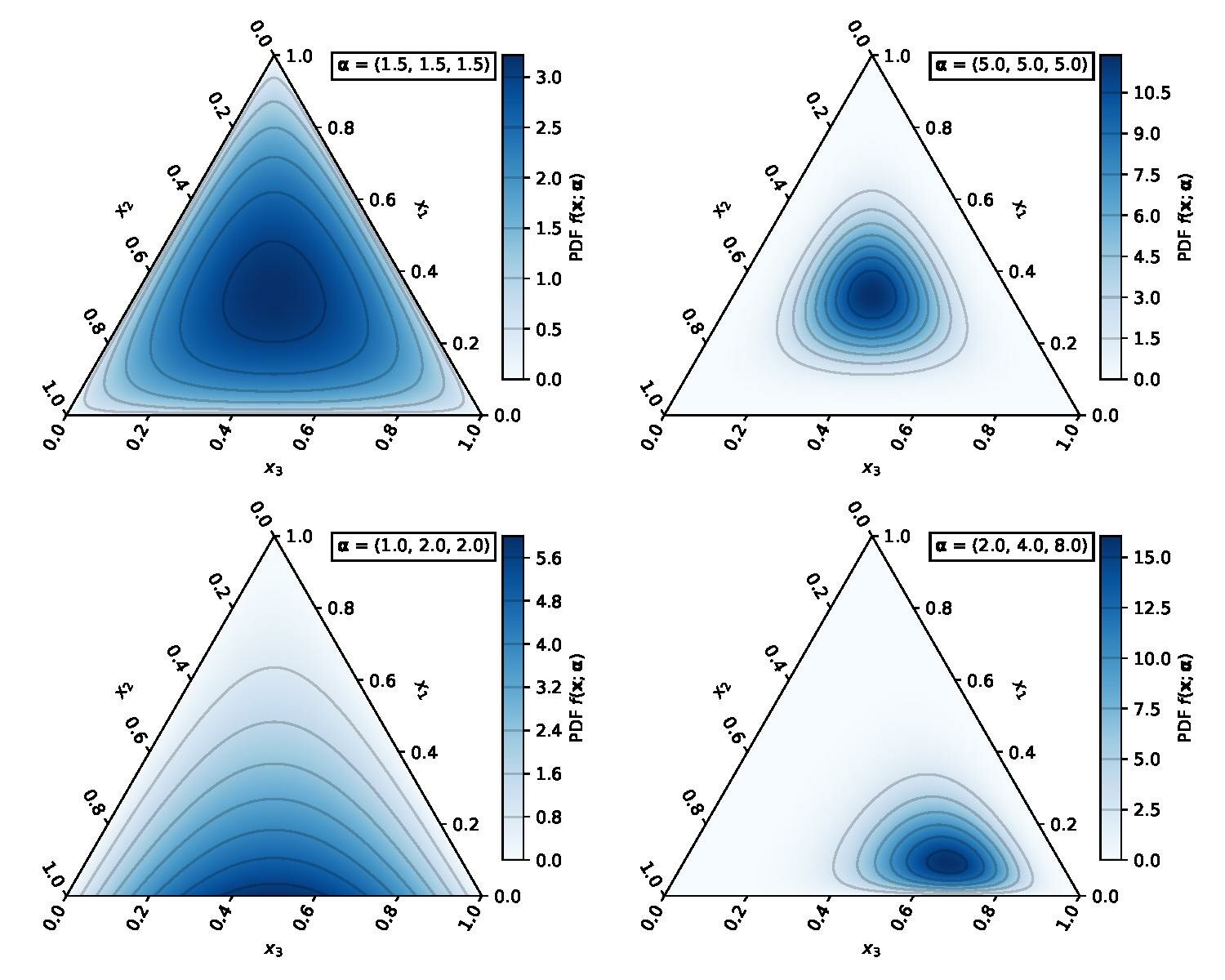
Dirichlet distribution
In probability and statistics, the Dirichlet distribution, often denoted , is a family of continuous multivariate probability distributions parameterized by a vector of positive reals. It is a multivariate generalization of the beta distribution, hence its alternative name of multivariate beta distribution (MBD). Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact, the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution.
https://en.wikipedia.org/wiki/Dirichlet_distribution
