의미적 이해
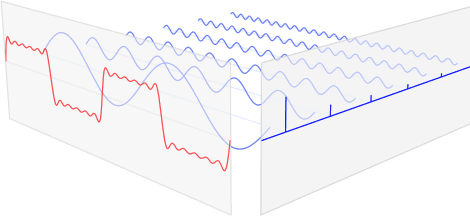
푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현

맨 앞의 붉은 색 신호는 입력 신호이고 뒤의 파란색 신호들은 푸리에 변환(Fourier transform)을 통해 얻어진 (원본 신호를 구성하는) 주기함수 성분들이다
입력 신호는 전파, 음성 신호 등과 같이 시간축(time)에 대해 정의된 신호일 수도 있고 이미지(image) 등과 같이 공간축에 대해 정의된 신호일 수도 있다
time domain에서 frequency domain으로의 변환이라고 하고
컴퓨터 비전(computer vision),영상처리 쪽에서는 spatial domain에서 frequency domain으로의 변환이라고 부른다
수식적 이해

푸리에 역변환
함수 f(x)를 모든 가능한 주파수(u)의 주기함수들(ej2πux)의 일차결합으로 표현한 것

푸리에 변환
입력신호 f(x)가 ej2πux들의 합으로 표현(분해)된다
f(x)를 주기함수 성분으로 분해했을 때의 계수(coefficient) F(u)로 주어진다
ej2πux는 f(x)를 구성하는 (파란색의 주파수 u인) 주기함수 성분들이고 F(u)는 해당 주기함수 성분의 강도(amplitude)를 나타낸다

오일러 공식과 자주 같이 쓰인다

이렇게 변형된다
결국 ej2πux는 주파수 u인 정현파(sinusoidal wave)의 복소지수함수 표현
선형대수적으로 이해하자면 ej2πux, u = 0, ±1, ±2, ...은 모든 신호를 생성할 수 있는 직교(orthogonal) 기저(basis) 함수들로 볼 수 있다 (편의상 u를 정수 범위로 표기했으나 u는 실수 전체 범위임)
그러면 입력 신호 f(x)를 이들 기저함수들로 분해했을 때의 계수 F(u)는 f(x)와 기저함수의 내적(dot product)으로 계산될 수 있다
f(x)와 ej2πux의 함수 내적이기 때문에 그 결과는 f(x)를 ej2πux들로 분해했을 때의 계수가 된다
페이저(phasor)
우선 phasor에 대해 정확히 이해하기 위해선 다음의 개인정리를 꼭 읽기 바람. 또는 아래의 내용에 대해 알고 있는 사람이라면 계속 공부하셔도 무방합니다. ① 허수란 무엇인가? ② 자연상수 e의 존재 의미 ③ 오일러 공식의 유도과정과 그 의미 푸리에 분석의 최종적 결론이라고 할 수 있는 모든 신호는 정현파의 합으로 나타낼 수 있다는말은 학부시절 귀 따갑게 들었던 말이다 (독자가 현재 학부 과정 중에 있다면 귀에 따갑게 듣게 될 것이다.).
https://angeloyeo.github.io/2019/06/18/phasor.html
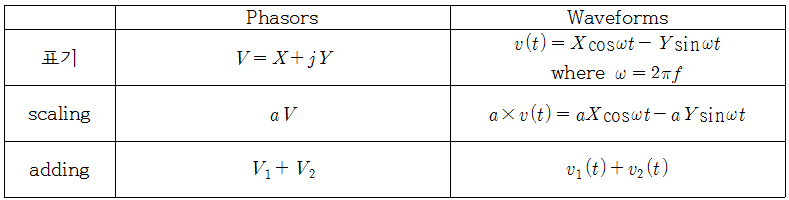
푸리에 급수의 시작(Fourier Series)
그림 1] 푸리에 급수를 이용한 톱니파의 표현(출처: wikipedia.org) 여기서 $F_{-m} = -F_m$, 첫째식은 어떤 함수 $(\cdot)$를 한 주기 $T$에 대해 ( 적분(integration)이다. 기함수를 한 주기에 대해 적분하면 둘째식에 있는 사인 함수 sine function)의 직교성(orthogonality: 서로 다른 두 함수를 곱해 적분하면 항상 0이 되는 성질)에 의해 셋째식이 얻어진다.
https://ghebook.blogspot.com/2012/07/fourier-series.html
Fourier Transform(푸리에 변환)의 이해와 활용
푸리에 변환(Fourier transform)에 대해서는 예전부터 한번 정리를 해야겠다고 생각만 했었는데 이번에 기회가 되어 글을 올립니다. 푸리에 변환(Fourier transform)은 신호처리, 음성, 통신 분야에서 뿐만 아니라 영상처리에서도 매우 중요한 개념으로 다양한 응용을 가지고 있습니다. 영상을 주파수 성분으로 변환하여 다양한 분석 및 처리를 할 수 있고 임의의 필터링 연산을 fft(fast Fourier transform)를 이용하여 고속으로 구현할 수도 있습니다.
https://darkpgmr.tistory.com/171

 Seonglae Cho
Seonglae Cho