Quadratic form Property
Important application of positive definiteness is Convex Optimization. For a twice differentiable real-valued function f, if the Hessian matrix is a positive definite matrix, then the overall shape of this function is convex downward, and it necessarily has a global minimum. If we calculate the gradient here and find the point where it is zero, that point is precisely the local minimum. This is the multivariate version of the second derivative test for Convex function.
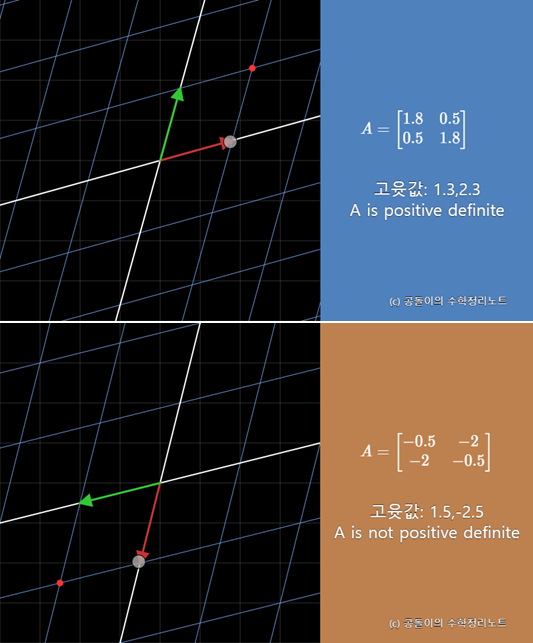
Negative definite Matrix
Positive Definite matrix
Positive semi-definite matrix
Negative semi-definite matrix
Definite matrix
In mathematics, a symmetric matrix
 
M
 
{\displaystyle \ M\ }
with real entries is positive-definite if the real number
 
x
⊤
M
x
 
{\displaystyle \ \mathbf {x} ^{\top }M\mathbf {x} \ }
is positive for every nonzero real column vector
 
x
 
,
{\displaystyle \ \mathbf {x} \ ,}
where
 
x
⊤
 
{\displaystyle \ \mathbf {x} ^{\top }\ }
is the row vector transpose of
 
x
 
.
{\displaystyle \ \mathbf {x} ~.}
[1]
More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number
 
z
∗
M
z
 
{\displaystyle \ \mathbf {z} ^{*}M\mathbf {z} \ }
is positive for every nonzero complex column vector
 
z
 
,
{\displaystyle \ \mathbf {z} \ ,}
where
 
z
∗
 
{\displaystyle \ \mathbf {z} ^{*}\ }
denotes the conjugate transpose of
 
z
 
.
{\displaystyle \ \mathbf {z} ~.}
https://en.wikipedia.org/wiki/Definite_matrix
양의 정부호 (positive definite) 행렬
글로 정리된 곳: https://angeloyeo.github.io/2021/12/20/positive_definite.html---커피 한 잔의 후원이 큰 힘이 됩니다.후원하기(카카오페이): https://qr.kakaopay.com/281006011000018389112430후...
https://www.youtube.com/watch?v=fuxJ-VH8pWk

양의 정부호 행렬 (positive definite matrix)
양의 정부호 행렬에 대해 더 잘 알기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다. 우선 양의 정부호 (positive definite) 행렬의 정의부터 차근히 살펴보도록 하자. 영벡터가 아닌 임의의 열벡터 $x$와 대칭 행렬 $A$에 대해 다음이 성립한다면 $A$는 양의 정부호(positive definite) 행렬이다. \[x^TAx >0\] 생각해보면 굉장히 이상한 정의다.
https://angeloyeo.github.io/2021/12/20/positive_definite.html

 Seonglae Cho
Seonglae Cho