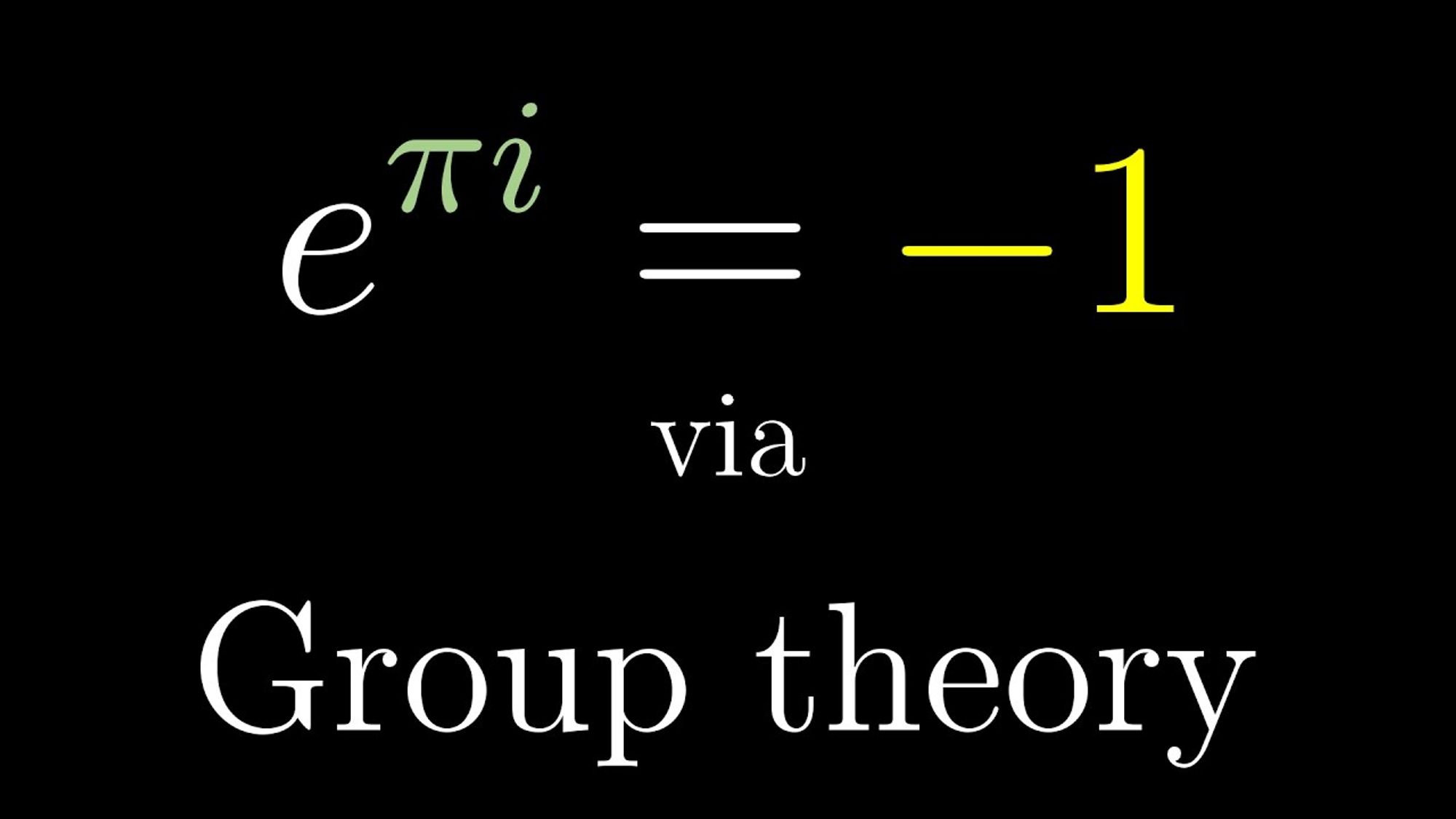Seonglae ChoGroup-like Structure
Group is a set of operations which can be combined or reversed
Groups are very useful for describing the Symmetry
They allow us to view the symmetry of mathematical objects from a common perspective
When a set is closed under a binary operation, it satisfies the associative law and every element has an identity element and an inverse
Group theory Notion
Group theory
In abstract algebra, group theory studies the algebraic structures known as groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.
https://en.wikipedia.org/wiki/Group_theory
An Introduction To Group Theory
I hope you enjoyed this brief introduction to group theory and abstract algebra.
If you'd like to learn more about undergraduate maths and physics make sure to subscribe!
https://www.youtube.com/watch?v=zkADn-9wEgc
Euler's formula with introductory group theory
Intuition for e^(πi) = -1, using the main ideas from group theory
Help fund future projects: https://www.patreon.com/3blue1brown
An equally valuable form of support is to simply share some of the videos.
Special thanks to these supporters: http://3b1b.co/epii-thanks
Additional support for this video came from Emerald Cloud Lab:
https://www.emeraldcloudlab.com/
There's a slight mistake at 13:33, where the angle should be arctan(1/2) = 26.565 degrees, not 30 degrees. Arg! If anyone asks, I was just...er...rounding to the nearest 10's.
For those looking to read more into group theory, I'm a fan of Keith Conrad's expository papers: http://www.math.uconn.edu/~kconrad/blurbs/
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommended
Various social media stuffs:
Website: https://www.3blue1brown.com
Twitter: https://twitter.com/3Blue1Brown
Patreon: https://patreon.com/3blue1brown
Facebook: https://www.facebook.com/3blue1brown
Reddit: https://www.reddit.com/r/3Blue1Brown
https://youtu.be/mvmuCPvRoWQ
0으로 나누어 보았습니다.
0으로 나누는 문제는 수학에서 까다로운 이슈입니다. 하지만 군, 환, 체를 이용하면 이 문제를 다룰 수 있는 방법이 있습니다. 영환(Zero Ring)은 모든 원소가 0인 환으로, 이를 통해 0으로 나누는 연산을 정의할 수 있습니다. 또한 바퀴이론(Wheel Theory)을 사용하면 원소를 추가하여 0으로 나누는 연산을 더 일반적인 방법으로 다룰 수 있습니다.
• blog : https://rayc20.tistory.com/334
• 교육 목적으로 영상 및 블로그 자료를 자유롭게 사용하셔도 좋습니다.
• 외주 및 광고 관련 문의는 받지 않습니다.
#수학 #나누기 #0 #대수 #현대대수학 #추상대수학
0:48 연산이란 무엇인가?
1:03 군(Group)
5:49 환(Ring)과 체(Field)
6:36 사칙연산
8:14 Zero Ring
9:29 0으로 나누면 무한대?
9:55 One-Point Compactification
12:00 Wheel Theory
16:31 에필로그
https://www.youtube.com/watch?v=n9BuGfCs5N4
