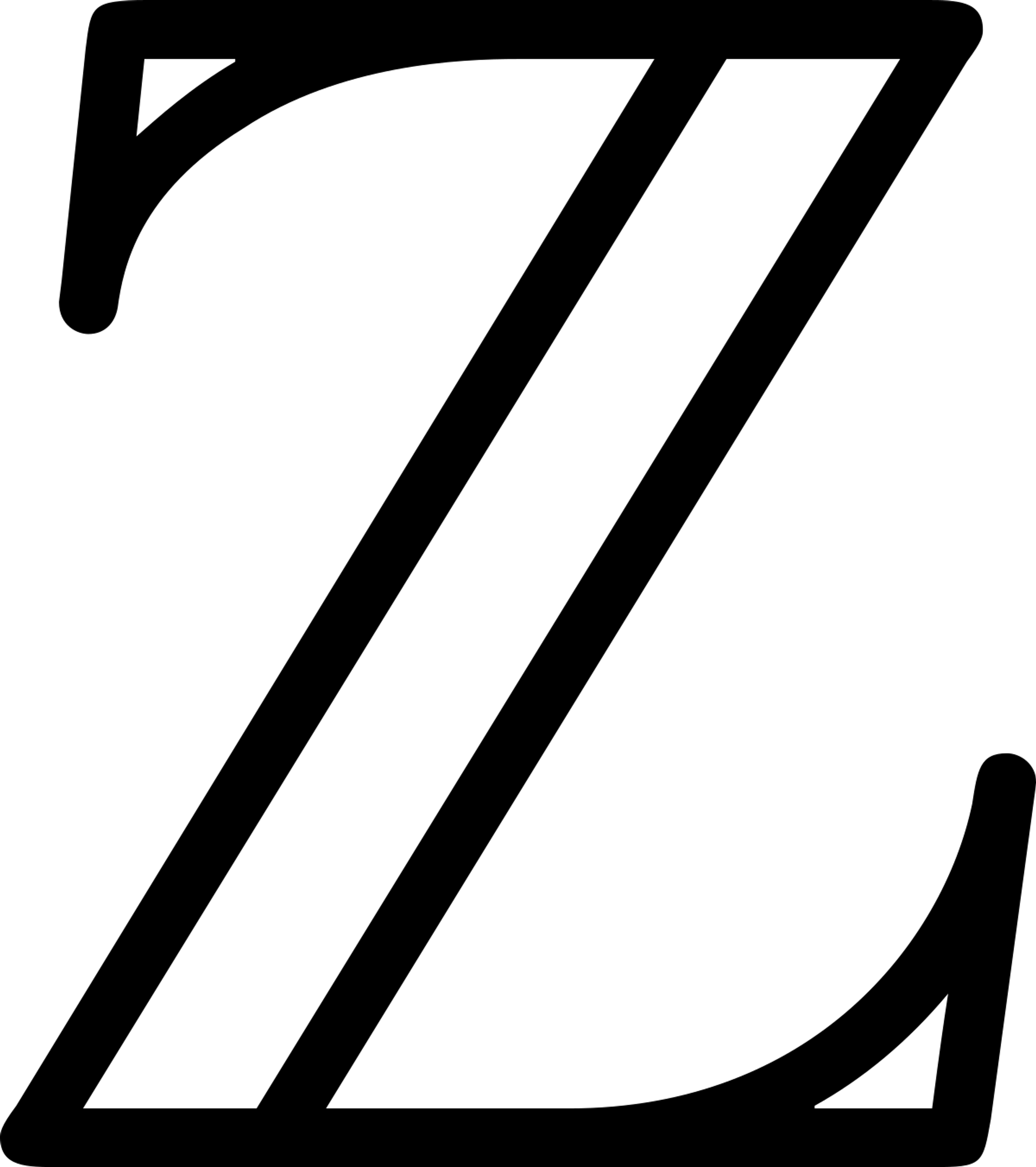Ringoids, Ring-like structures
A ring is a set equipped with two binary operations (typically called addition and multiplication) where the set forms an Abelian Group under addition (closed) and a Semigroup under multiplication (closed). Semi Group
Ring theory Notion

 Seonglae Cho
Seonglae Cho