Seonglae ChoA formal system for dealing with logical operations such as abstraction and function application
Lambda calculus is a concept of 'pure function' proposed by Alonzo Church, defining computation using only variables and function application. It corresponds to the
Function in Wolfram Language - Terms in lambda calculus are constructed through variables, abstraction, and application operations
- The Greek letter lambda (λ) is used as the symbol for abstraction
- Operations such as alpha equivalence and beta reduction can be performed on lambda calculus terms
- Alpha equivalence is a transformation that changes bound variables to prevent name collisions
- Beta reduction is a transformation that replaces function application with the result of appropriate substitution operations
Lambda calculus enables a simple expression of functions, providing deeper insights into the concept of 'function computation'
Lambda Calculus Notion
Lambda Calculus Usage
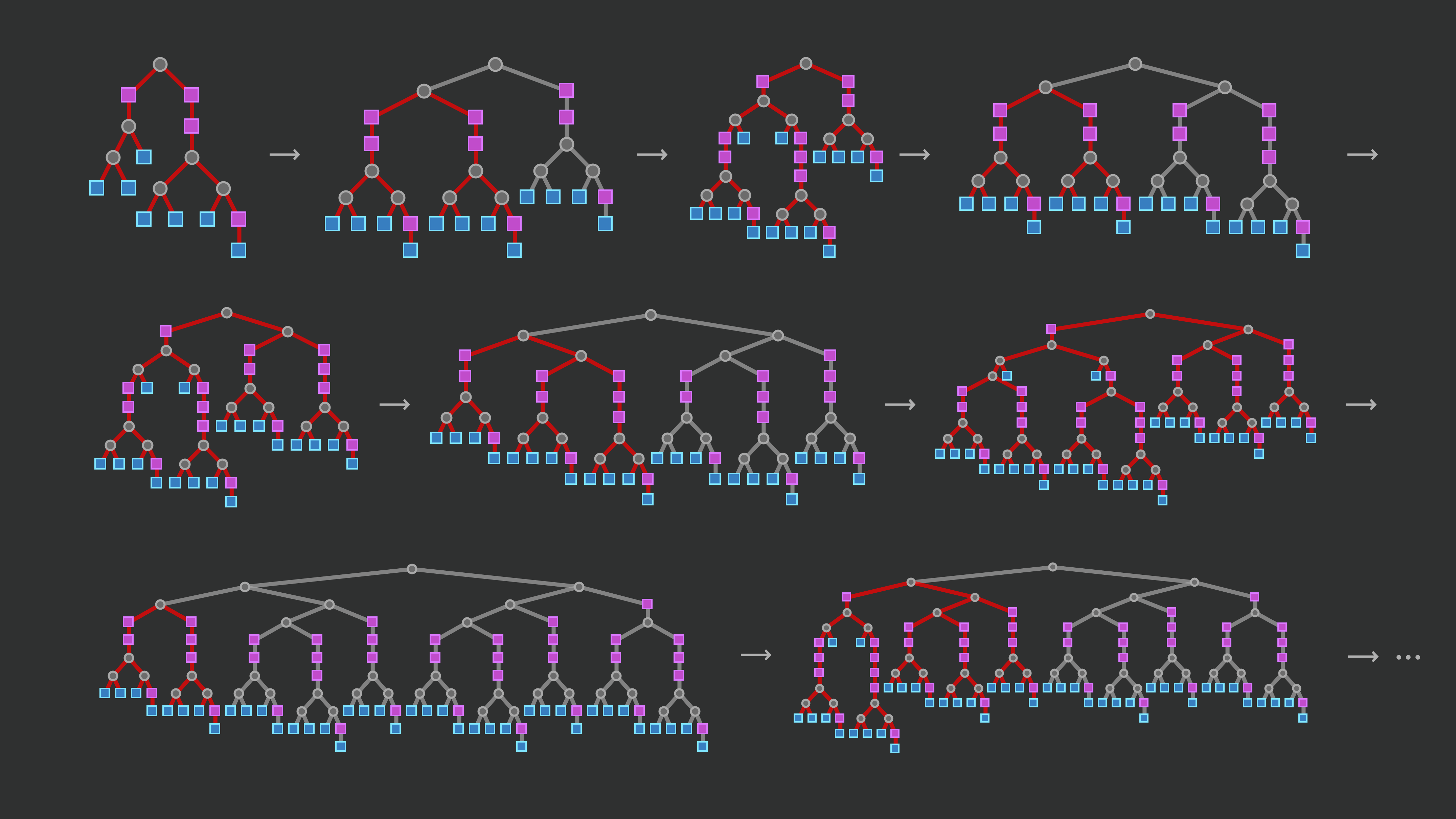
The Ruliology of Lambdas
Stephen Wolfram explains the rich ruliology of lambdas, made particularly significant by their connection to practical computing. Covers basic computations to undecidability to multiway graphs and evaluation strategies.
https://writings.stephenwolfram.com/2025/09/the-ruliology-of-lambdas/
