Absolute Positional Encoding

d is model embedding dimension

i is index of embedding vector

p is token position of input text

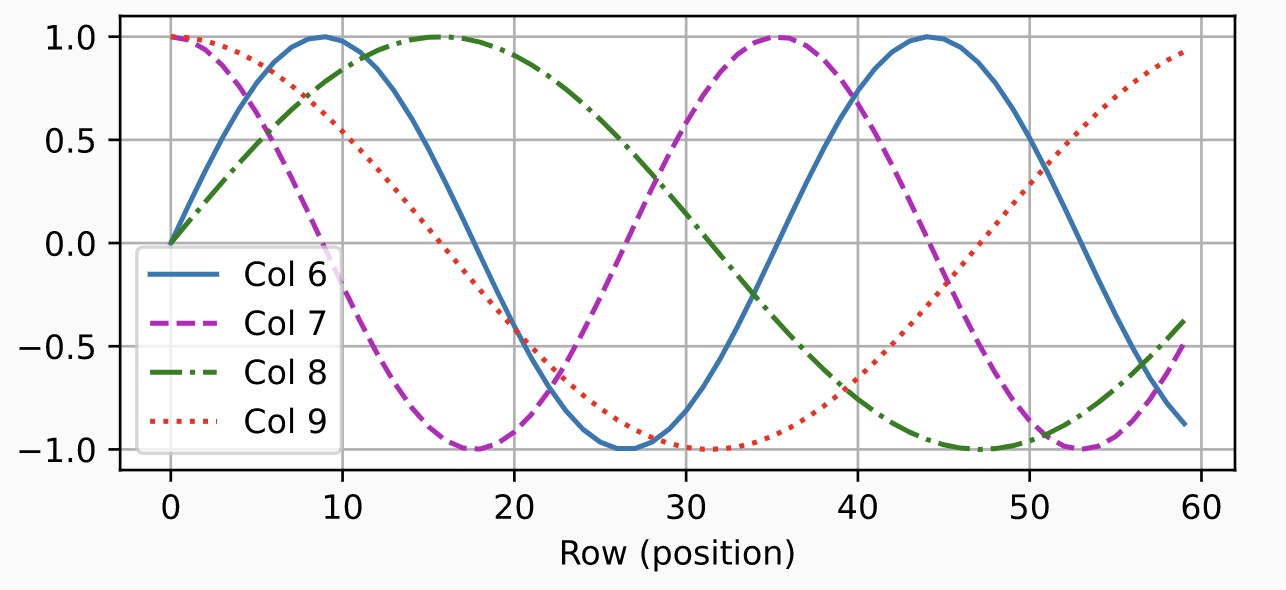
Overall, different frequencies are assigned to each position to make them recognizable, and using different even/odd functions (sine/cosine) creates phase differences that make each position distinctly identifiable

Key points of the formula below

Designed to consider exponential positions according to embedding dimension

Separates high and low frequencies to distinguish positions through frequency

In theory, it can distinguish exponential positions relative to the model embedding depth

Ultimately, attention weights fit to this mathematical position encoding. The design of this function only needs to ensure that embeddings are distinguishable from each other

Papers with Code - Absolute Position Encodings Explained

Absolute Position Encodings are a type of position embeddings for [Transformer-based models] where positional encodings are added to the input embeddings at the bottoms of the encoder and decoder stacks. The positional encodings have the same dimension $d_{model}$ as the embeddings, so that the two can be summed. In the original implementation, sine and cosine functions of different frequencies are used: $$ \text{PE}\left(pos, 2i\right) = \sin\left(pos/10000^{2i/d_{model}}\right) $$ $$ \text{PE}\left(pos, 2i+1\right) = \cos\left(pos/10000^{2i/d_{model}}\right) $$ where $pos$ is the position and $i$ is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from $2\pi$ to $10000 \dot 2\pi$. This function was chosen because the authors hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $\text{PE}_{pos+k}$ can be represented as a linear function of $\text{PE}_{pos}$. Image Source: D2L.ai