MCMC

Creator

Creator

Alan Jo

Created

Created

2022 Apr 3 15:8

Editor

Editor

Alan Jo

Edited

Edited

2023 Nov 21 11:26

Refs

Refs

Markov Chain

Monte Carlo Method

Metropolis Algorithm

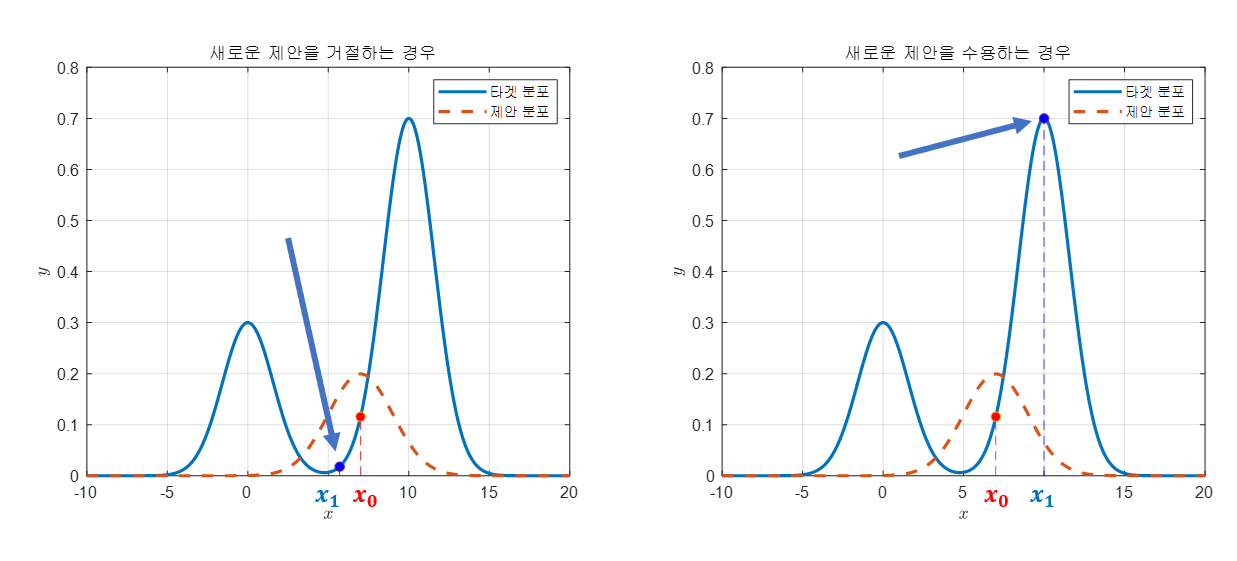
Markov chain Monte Carlo

통계적인 특성을 이용해 무수히 뭔가를 많이 시도해본다는 의미로 Monte Carlo라는 이름

통계학의 특성 상 무한히 많은

Simulation을 거쳐야만 진짜 정답이 뭔지 알 수 있지만, 그렇게 하기가 현실적으로 어렵기 때문에 Finite 시도만으로 정답을 추정하자

첫 샘플을 랜덤하게 선정한 뒤, 첫 샘플에 의해 그 다음번 샘플이 추천되는 방식의 시도 반복

여기서 추천되는 방식이 각자 다르고 Markov chain에서 Monte Carlo는 Metropolis Algorithm 이용

MCMC Notion

Markov Chain Monte Carlo

Interactive MCMC JS Applet by Chi-Feng, 소스코드 이 포스팅에 대해 잘 이해하기 위해선 다음의 내용에 대해 알고 오시는 것이 좋습니다. 위키피디아에 따르면 마르코프 연쇄 몬테카를로 방법(Markov Chain Monte Carlo, MCMC)은 "마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출하는 알고리즘의 한 분류이다."라고 나와있다.

Markov Chain Monte Carlo

https://angeloyeo.github.io/2020/09/17/MCMC.html

Markov Chain Monte Carlo

en.wikipedia.org

https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo

Recommendations

///////