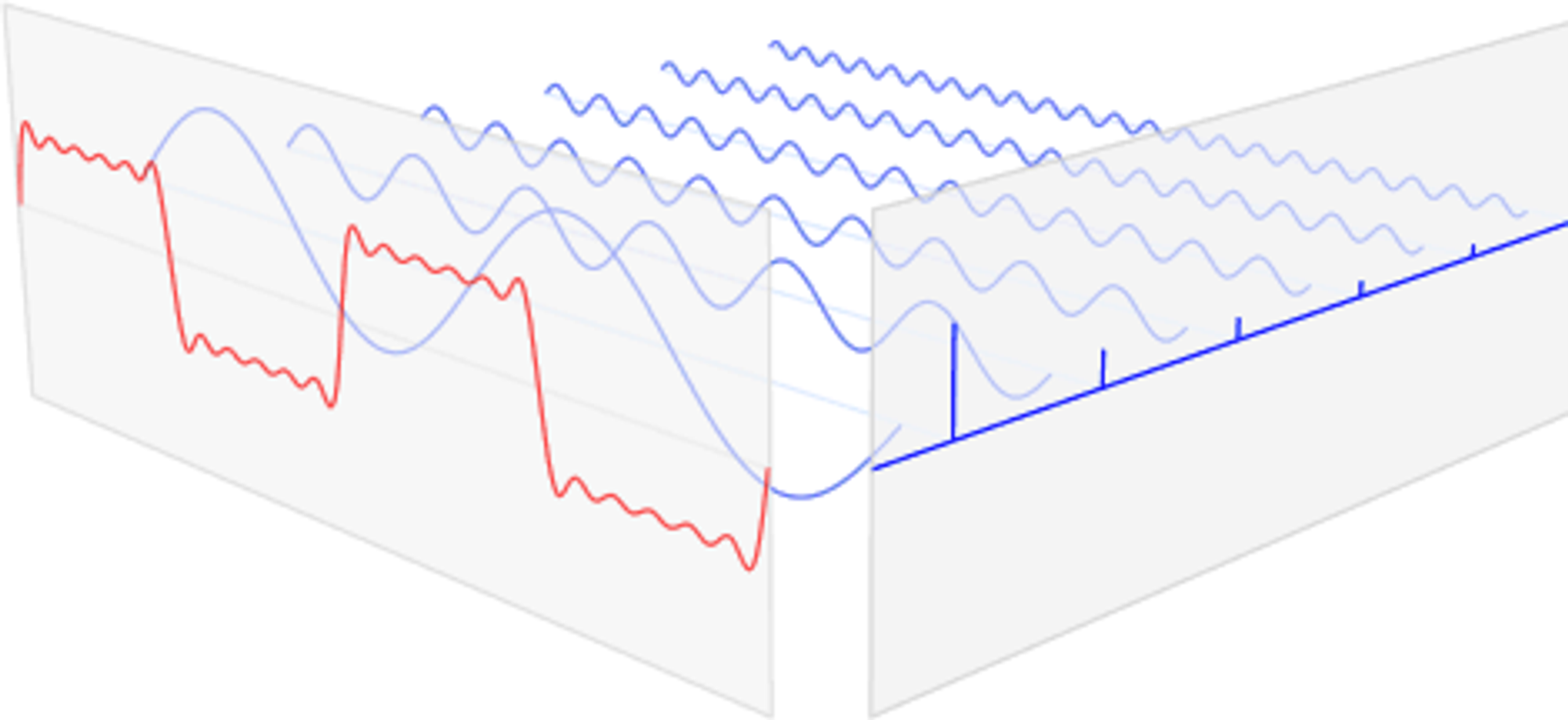
Linear transformation between time signal vector & frequency vector
The Wavelet Transform is a means of moving between Locality and Universality preserving properties, while Fourier Transform’s frequency-based representation is merely one efficient choice.
Unlike Fourier Series we do not use Periodic signal Tilda function. By Fourier Transform out purpose is transforming aperiodic signal to periodic signal. We let the infinite long period for representing Fourier transform. and then goes to 0, then become a variable.
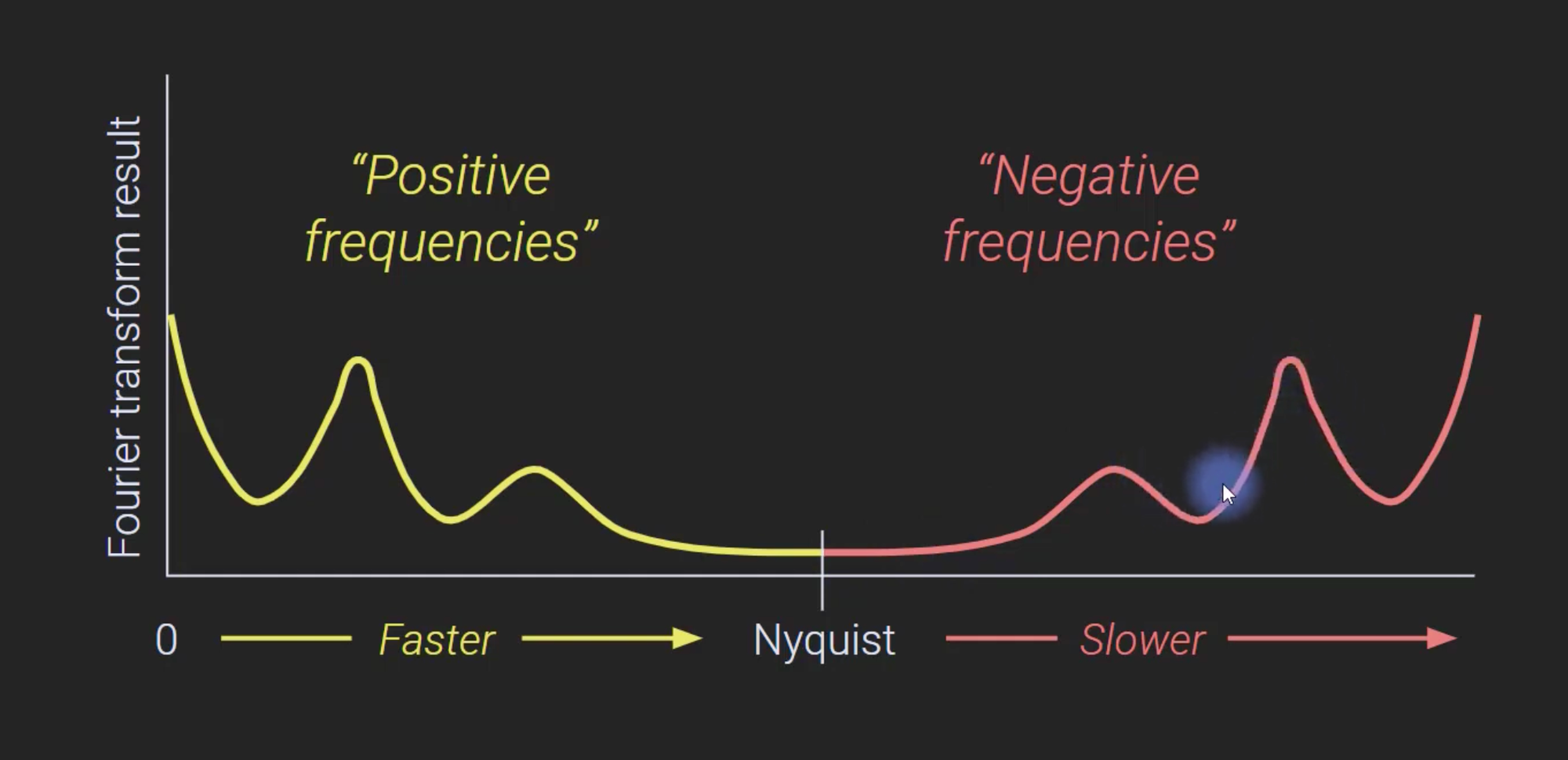
In the non-periodic case, the set of frequencies becomes continuous, meaning that there are an infinite number of frequencies present. This is because non-periodic signals cannot be represented as a sum of harmonically related sinusoids, which is the case for periodic signals. Instead, non-periodic signals can be represented as a sum of sinusoids with continuously varying frequencies.
Fourier transform
Inverse Fourier transform
Fourier Transform Notion
Fourier Transform Usages
